En muchos juegos se necesita en algún momento lanzar proyectiles. En esta guía exploraremos la física detrás de estos tiros de cara a realizar una implementación sencilla de tiros parabólicos sin necesitar bibliotecas de física especializadas.
Para empezar con algo simple, consideremos que nuestro juego tiene dos dimensiones: altura y profundidad.
Introducción a los vectores
En física, a menudo se encuentran casos donde una magnitud (cantidad) y una dirección están intimamente relacionadas a la hora de describir un fenómeno. Un ejemplo clásico es la velocidad: es tan importante la magnitud de la velocidad de un coche (habitualmente medida en km/h) como en qué dirección se está moviendo.
Cuando se dan estas relaciones es habitual tratar magnitud y dirección de manera conjunta. Cuando una variable matemática representa estos dos conceptos simultáneamente, se le denomina vector y se representa colocando una flecha encima del nombre de la variable, por ejemplo, $\vec{v}$.
Hay dos formas habituales de expresar el valor de un vector. Una forma es indicar la magnitud y la dirección (ángulo) expresamente. Por ejemplo:
$$\vec{v} = 100_{60^{\circ}}\space km/h$$
Esta fórmula representaría la velocidad de un coche que se mueve a 100 km/h en dirección 60º. (medidos con respecto a un ángulo que consideremos origen, por ejemplo el Norte geográfico y en un determinado sentido). Cuando usemos ángulos en vectores debemos tener en cuenta siempre qué dirección consideraremos como referencia y en qué sentido haremos la medición. Por ejemplo, en este caso podríamos considerar que el ángulo se mide en grados desde el Norte geográfico hasta la posición a medir girando en sentido de las agujas del reloj.
En matemáticas, una convención habitual es considerar que 0º es el plano horizontal y los ángulos positivos están en el sentido contrario a las agujas del reloj, por ejemplo:
Otra forma de expresar un vector es descomponer magnitud y dirección en coordenadas. Por ejemplo:
$$\vec{v} = (30, 50)\space km/h$$
En este caso estaríamos representando la velocidad de un coche que cada hora avanza 30 km en el eje horizontal (x) y 50 km en el eje vertical (y). Los ejes horizontal y vertical se pueden representar también como vectores, habitualmente con los nombres $\vec{i}$ y $\vec{j}$ para los ejes $x$ e $y$ respectivamente. Por ejemplo, el mismo vector anterior se podría representar como:
$$\vec{v} = 30\vec{i} + 50\vec{j}\space km/h$$
Cada representación tiene sus ventajas e inconvenientes. En nuestros ejemplos utilizaremos la representación de coordenadas, con una variable por coordenada, por ejemplo: velX, velY. En esta representación es muy fácil sumar vectores.
Objetos
Para incorporar física en nuestros objetos debemos añadirles propiedades que reflejen el estado de todas las variables físicas que sean de nuestro interés. En este caso necesitamos, como mínimo:
- Posición (x, y): Dónde está el objeto en este momento.
- Velocidad (vector): Hacia dónde se mueve el objeto y cómo de rápido lo hace.
Cada objeto de nuestro juego deberá tener una función de actualización donde sus variables físicas sean actualizadas. Esta función será ejecutada de manera periódica, típicamente una vez por frame.
En nuestro ejemplo, la función de actualización se encargaría de actualizar la posición en función de la velocidad. Si la velocidad del objeto es 2 píxels por frame y la función de actualización se ejecuta cada frame, deberá sumarse 2 a la posición del objeto.
function update() {
this.posX = this.posX + this.velX;
this.posY = this.posY + this.velY;
}Lanzar un proyectil
Lanzar un proyectil consiste en aplicarle una velocidad.
Sin ninguna fuerza que modifique la trayectoria del proyectil, éste se moverán línea recta.
Es posible que en este paso necesitemos convertir una velocidad expresada en magnitud y dirección a formato de componentes $x$ e $y$. Para ello podemos hacer uso de trigonometría básica:
function shoot(speedMagnitude, speedDirection) {
this.velX += speedMagnitude * Math.cos(speedDirection);
this.velY += speedMagnitude * Math.sin(speedDirection);
}Gravedad
En el mundo real, los objetos en movimiento están sometidos a fuerzas, que los aceleran en determinadas direcciones. Particularmente, la gravedad cada usa que los proyectiles caigan.
Para objetos en la Tierra de una masa pequeña comparada a la de un planeta, la aceleración causada por la gravedad es constante y conocida: 9,8 $m/s^2$.
Esto significa que cada segundo, la velocidad del objeto se incrementa en 9,8 $m/s$ (metros por segundo) en dirección al centro de la Tierra. Cuanto más tiempo lleva cayendo, más rápido cae.
Por supuesto este movimiento cesa cuando el objeto llega al suelo. (Realmente la gravedad sigue haciendo su trabajo, pero aparece una fuerza de tensión en sentido contrario ejercida por el suelo que causa que el objeto no se hunda.)
Debemos tener en cuenta esto en nuestros programas para que nuestros objetos no caigan al eternamente al vacío (salvo que sea eso exactamente lo que queramos).
Para tener en cuenta la gravedad modificaremos la velocidad en nuestra función de actualización. Por ejemplo:
function update() {
//En este ejemplo asumimos que y=0 es el suelo y las
// y's positivas están encima del suelo.
// La gravedad modifica la velocidad del objeto,
// siempre que no esté en el suelo.
if (this.y > 0) {
var gravity = 9.8; // píxels/frame²
this.velY = this.velY - gravity;
}
// Movemos el objeto de acuerdo a su velocidad.
this.posX = this.posX + this.velX;
// Utilizamos la función máximo para que el objeto
// no pueda caer a una posición subterránea.
this.posY = Math.max(this.posY + this.velY, 0);
}Demostración
En la siguiente demo se muestran una pequeña aplicación del tiro parabólico.
Extra: Rotación de proyectiles
Muchos proyectiles, por su forma aerodinámica, giran sobre sí mismos conforme avanzan en su trayectoria. Es el caso de las flechas empleadas en la demostración anterior. Si no fuera por esta rotación, el movimiento sería algo extraño, como en la imagen siguiente:
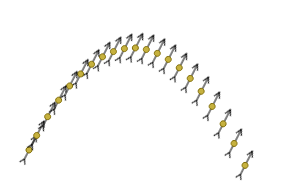
En lugar de eso queremos algo así, como vimos en la demo:

Afortunadamente, este efecto es fácil de simular. Observa la siguiente ilustración de la posible trayectoria de una flecha.
Los círculos rosados señalan los puntos de la trayectoria que realmente aparecerían en nuestro juego. Aunque en teoría la trayectoria tiene infinitos puntos, nuestro juego tendrá que conformarse con representar sólo algunos. Esto es lo que hacemos cuando actualizamos la posición de nuestros objetos sólo 60 veces por segundo. Por supuesto, en la imagen este efecto está muy exagerado.
Si trazamos una línea entre dos puntos consecutivos obtendremos la inclinación que queremos para nuestro proyectil cuando se halle sobre uno de esos puntos de forma bastante precisa. A mayor sea la resolución (más cerca estén esos puntos), mayor será la precisión.
Habiendo visto esto, el procedimiento es muy fácil. Sólo necesitamos conocer cómo ha cambiado nuestra posición durante el frame actual, o dicho de otro modo, en qué dirección nos estamos moviendo. Esto nos lo da el vector velocidad.
Teniendo un vector que indica nuestra dirección, es muy fácil extraer su ángulo utilizando razones trigonométricas. El ángulo del vector velocidad será el ángulo de rotación de nuestro proyectil.
Cálculo del ángulo de un vector
El ángulo de un triángulo representado arriba se determina mediante la función arcotangente (abreviada $atan$), que a su vez es la inversa de la función tangente (abreviada $tan$ o $tg$).
La función tangente de un ángulo se define como la división de la longitud del cateto opuesto a ese ángulo entre la longitud del cateto contiguo.
$$tan(\alpha) = \frac{cateto\ opuesto}{cateto\ contiguo}$$
La arcotangente nos da la información contraria: a partir de la división del cateto opuesto y el cateto contiguo nos da el ángulo.
$$atan\bigg( \frac{cateto\ opuesto}{cateto\ contiguo} \bigg) = \alpha$$
La función arcotangente viene implementada en todos los lenguajes de programación de uso común. Sin embargo, tiene un defecto: sólo devuelve ángulos entre -90° y 90°. Esto es debido a que al hacer la división de cateto opuesto entre cateto contiguo estamos perdiendo información. Por ejemplo, basta con que uno de ellos sea negativo para que el resultado sea también negativo, y a partir del resultado no podemos determinar el signo de los operandos.
Para obtener un ángulo entre 0° y 360° (o lo que es lo mismo entre -180° y 180°) debemos tener en cuenta el signo de los catetos del triángulo. Por ejemplo, si el cateto horizontal es negativo y el vertical es positivo, será necesario sumar 90° al ángulo devuelto por la arcotangente. Además con la función de arcotangente que tener un cuidado especial, ya que si el cateto contiguo es cero se producirá una excepción de división por cero.
Debido a todos estos casos especiales, y siendo un problema muy habitual necesitar calcular un ángulo a partir de sus catetos, la mayoría de lenguajes de programación implementan una función atan2 (definición en Wikipedia) que recibe en parámetros separados la longitud del cateto opuesto y la longitud del cateto contiguo, encargándose la misma función de ajustar el valor de retorno en función del signo de los argumentos, así como de los valores límite.
Su uso es muy sencillo. $y$ es la longitud del cateto opuesto (habitualmente altura) y $x$ la del cateto contiguo (habitualmente anchura). Cualquiera de ellos negativos si están al otro lado del origen de coordenadas:
$$atan2(y, x) = \alpha$$
Función de actualización
A continuación se muestra una función de actualización que actualiza la rotación del proyectil durante su trayectoria utilizando el método explicado:
function update() {
// En este ejemplo asumimos que y=0 es el suelo y las
// y's positivas están encima del suelo.
// La gravedad modifica la velocidad del objeto,
// siempre que no esté en el suelo.
if (this.y > 0) {
var gravity = 9.8; // píxels/frame²
this.velY = this.velY - gravity;
}
// Movemos el objeto de acuerdo a su velocidad.
this.posX = this.posX + this.velX;
// Utilizamos la función máximo para que el objeto
// no pueda caer a una posición subterránea.
this.posY = Math.max(this.posY + this.velY, 0);
// Actualizamos la rotación del objeto
this.angle = Math.atan2(this.velY, this.velX);
}

